|
| Positioning of the canonical sensor |
|
ALE
Image Processing Software Deblurring, Anti-aliasing, and Superresolution. Local Operation localhost 5393119533 |
[ Up | Merging | Drizzling | Enhancement | Irani-Peleg | Alignment ]
ALE combines a series of input frames into a single output image possibly having:
This page provides information on related work, models of program input, an outline of renderers, and an overview of the algorithm used in ALE.
Note: This document uses PNGs and HTML 4 character entities.
Steve Mann's work in Video Orbits on increased spatial extents and the use of projective transformations has influenced features incorporated by ALE.
ALE incorporates an iterative solver based on the work of Michal Irani and Shmuel Peleg on image reconstruction.
Using R+ to represent the non-negative real numbers, a discrete image D of size (d1, d2) is a function
D: {0, 1, …, d1 - 1}×{0, 1, …, d2 - 1} → R+×R+×R+A continuous image I of size (c1, c2) is a function
I: [0, c1]×[0, c2] → R+×R+×R+
In this document, a member of the set R+×R+×R+ is sometimes called an RGB triple.
A camera snapshot is defined as an n-tuple consisting of:
S represents a physical scene.
R represents the viewing volume of a physical camera.
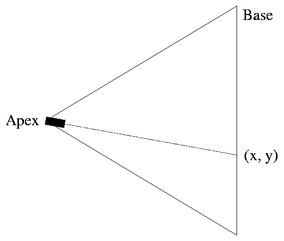
The value I(x, y) is the RGB triple representing the radiance that would be recorded from S by a directional light sensor located at the apex of R and aimed at the point (x, y) on the base of R. The only constraint on the sensor is that, given a fixed scene S, it must return a unique value for a given position and orientation. This sensor is assumed to be the same for all camera snapshots, and is called the canonical sensor.

|
| Positioning of the canonical sensor |
D represents the discrete pixel values reported by the camera.
The composite function composite(d, i) represents the optical and electronic properties of the camera.
For positive integer N, a sequence of camera snapshots { C1, C2, …, CN }, defined by the n-tuples { Cj = (Sj, Rj, Ij, Dj, ij, dj) } is a camera input frame sequence if, for all j and j', Sj = Sj' and ij = ij'.
If the view pyramids { R1, R2, …, RN } of a sequence of N camera input frames all share a common apex and can be enclosed in a single rectangular-base pyramid R sharing the same apex and having base edges parallel to the base edges of R1, then the smallest such R is the extended pyramid. Otherwise, the extended pyramid is undefined.
If a camera input frame sequence has an extended pyramid R, then an extended image is defined from R in a manner analogous to the definition of the image I from the view pyramid R in the definition of a camera snapshot.
A projective snapshot is defined as an n-tuple consisting of:
Σ represents the subject of the snapshot (somewhat analogous to S in the camera snapshot).
D represents discrete pixel values reported by the physical imaging device.
For positive integer N, a sequence of projective snapshots { P1, P2, …, PN }, defined by the n-tuples { Pj = (Σj, Ij, Dj, qj, dj) } is a projective input frame sequence if, for all j and j', Σj = Σj'.
The first frame in the sequence of input frames is called the original frame, and subsequent frames supplemental frames.
From a camera input frame sequence, define a continuous image Σ as follows:
Cj = (S, Rj, Ij, Dj, i, dj)admits a projective input frame
Pj = (Σ, Ij, Dj, qj, dj)for some qj, and these { Pj } form a projective input frame sequence.
For a projective input frame sequence { Pj = (Σ, Ij, Dj, qj, dj) }, a projective renderer without extension is an algorithm that outputs a discrete image approximation of I1. The assumptions used in calculating the approximation vary across rendering methods.
For a projective input frame sequence { Pj = (Σ, Ij, Dj, qj, dj) }, a projective rendering method with extension is an algorithm that outputs a discrete image approximation of Σ. The assumptions used in calculating the approximation vary across rendering methods.
All renderers can be used with or without extension (according to whether the --extend flag is used). The target image for approximation (either Σ or I1) is generically called T.
Renderers can be of incremental or non-incremental type. Incremental renderers update the rendering as each new frame is loaded, while non-incremental renderers update the rendering only after all frames have been loaded.
Incremental renderers contain two data structures that are updated with each new frame: an accumulated image A with elements Ax, y and the associated weight array W with elements Wx, y. The accumulated image stores the current rendering result, while the weight array stores information about contributions to each accumulated image pixel.
Renderers should output approximations of T when certain predicates are satisfied. Not all of these predicates are required for all renderers, and renderers may produce acceptable output even when their predicates are not satisfied.
Predicate Explanation Alignment The projective input frame transformations qj are known. Translation All projective input frame transformations qj are translations. Point sampling with simple optics dj assigns Dj(x) = Ij(x). Very large, uniform input sequence A large number of input frames are provided, uniformly sampling the domain of T. Small radius The radius parameter used with the rendering method is chosen to be sufficiently small. Barlett filter approximation Convolution of T with a Bartlett filter remains an acceptable approximation of T. USM approximation Applying the unsharp mask employed by the ALE --hf-enhance option to the output of drizzling or merging produces an acceptable approximation of T. Correct Projection Filter The projection filter used in Irani-Peleg rendering approximates dj. Low Response Approximation Frequencies having low response in the Fourier domain representations of dj need not be accurately reconstructed in the Fourier domain representation of program output. Convergence Iterating Irani-Peleg on the input frames will eventually produce an acceptable approximation of T, and the number of iterations chosen is adequate to achieve this. This predicate may entail the very large, uniform input sequence predicate.
The following table indicates which rendering predicates are associated with each renderer. Note that renderers may produce acceptable output even when these predicates are not satisfied. Justification for non-obvious entries in this table should appear in the detailed descriptions; for entries where this is not the case, the value given should be considered unreliable.
M D H I Alignment X X X Translation X Point sampling with simple optics X X Very large, uniform input sequence X X Small radius X Barlett filter approximation X USM approximation X Correct Projection Filter X Low Response Approximation X X X X Convergence X
First, a merging renderer is instantiated. Then, program flags are used to determine what other renderers should be instantiated.
An iterative loop supplies to the renderers each of the frames in sequence, beginning with the original frame. The drizzling and merging renderers are incremental renderers, and immediately update their renderings with each new frame, while the high-frequency enhancement and Irani-Peleg renderers do not act until the final frame has been received.
In the case of the incremental renderers, the original frame is used without transformation, and each supplemental frame is transformed according to the results of the alignment algorithm, which aligns each new frame with the current rendering of the merging renderer.
Once all frames have been aligned and merged, non-incremental renderers produce renderings based on input frames, alignment information, and the output of other renderers.
Verbatim copying and distribution of this entire article is permitted in any medium, provided this notice is preserved.