ALE Version 0.7.x/0.8.x Technical Description

Purpose

This page discusses motivation, related work, models of program input, renderers, and the alignment algorithm, but does not cover the 3D scene reconstruction code in versions 0.7.2 and later. Note also that some changes in 0.8.x might not yet be covered. For information on ALE program operation and usage, see the User Manual for 0.7.x or 0.8.x.

Note: This document uses HTML 4 character entities. Sigma is 'Σ'; summation is '∑'.

Motivation

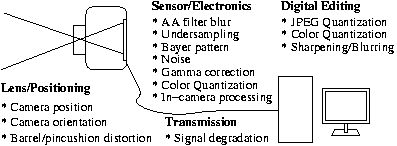
Several factors in the imaging pipeline can affect output, sometimes degrading image quality, either individually or through combination. Lens effects include barrel or pincushion distortion; the camera sensor and electronics can produce blurring, signal aliasing, noise, quantization, and non-linear effects; analog video signals can degrade in transmission; and various compression techniques and digital enhancements on- or off-camera can destroy image features. In some cases, a better image can be produced through combining information contained in different images.

Imaging Pipeline

Related Work

Richard Hook and Andrew Fruchter's drizzling technique was designed to combine dithered undersampled images. Previous versions of ALE supported this technique; the current version supports an approximation.

Steve Mann's work (e.g. here and here), on spatial extents, projective transformations, linear-colorspace image processing, and weighting by certainty functions, motivated ALE's adoption of these features. A modified, "one-sided" approach to certainty is used by ALE's Irani-Peleg renderer, to better accommodate extremely bright features that exceed the range of all input images. This approach is modified further in 0.8.0 to rely on estimated (instead of measured) intensities, which may allow further reduction of noise in some cases.

ALE incorporates an iterative solver based on Michal Irani and Shmuel Peleg's iterative deblurring and super-resolution technique. It has been extended to handle convolutions occurring in tandem in different colorspaces, and has been modified for certainty weighting.

ALE's treatment of barrel distortion, using a polynomial in distance from the image center, is based on that of Helmut Dersch's Panorama Tools. ALE's approach adjusts the linear (first-order) coefficient so that the corners of the transformed frame remain in place.

Program Inputs

Define an image to be a function mapping a subset of 2D Euclidean space to an RGB colorspace; define a discrete image to be an image defined only at coordinates having integral components; define a spatial discretization to be an operator that restricts the domain of an image to a set of points having integral components, thus producing a discrete image; define a spatial extension to be an operator that extends the domain of a discrete image by assigning the value of the nearest neighbor point.

Ignoring noise and color quantization, ALE assumes that each input frame d_x is a discrete image that can be obtained by applying a sequence of operators, including transformations, exposure adjustment, convolutions, gamma correction, spatial discretization, and spatial extension, to some image d, as follows:

d_x = DNCGDLE_xB_xP_xd

Where:

P_x is a projective transformation
B_x is a barrel/pincushion distortion transformation
E_x is linear exposure adjustment
L is a convolution in linear colorspace
D is a spatial discretization
G is gamma correction
C is a spatial extension
N is a convolution in non-linear colorspace

(When ALE aligns using Euclidean transformations, P_x are assumed to be Euclidean.)

The presence of an extension operator between G and N is suspect, and is somewhat inelegant in the case of digitally processed data, but although such extension may require careful selection of N, it does not restrict the set of possible models. It is only included because it creates a parallelism between N and L that makes implementation easier. In a more sophisticated implementation, it could be removed.

Incremental Rendering

If L and N are assumed to behave as identity operators, then each pixel in each input frame corresponds to a single point in d. In this case, it may be possible to apply filtering operations to input frame pixels directly. One caveat, however, is that different parts of the output may be sampled with unequal density in the input frame sequence; hence, a filtering approach that is uniform over all regions could cause significant aliasing or detail loss. Instead, ALE uses a non-uniform approach. If I_n(i, j) is an output pixel, at position (i, j), updated for input frames zero through n, then:

I_n(i, j) = ∑_n'∈0..n∑_{(i',j')∈Dom[d_n']} E_n'^-1G^-1d_n'(i',j') * c(n, n', i, j, i', j', E₀, ..., E_n, G, P₀, ..., P_n, B₀, ..., B_n, d₀, ..., d_n)

Where c is a rendering chain. Note that for most types of rendering chains, the above expression can be simplified considerably.

Irani-Peleg Rendering

ALE's Irani-Peleg renderer iteratively updates the final output of incremental rendering, with update operator U:

J₀ = I_final
J₁ = UJ₀
.
.
.
J_k = UJ_k-1

Where U is the Irani-Peleg update rule.

Spatial Extension and Space Complexity

By default, the output image is of fixed size, limited to the extents of d₀, the first image in the input sequence; the 'extend' option specifies that output should accommodate all regions of all input images.

When rendering an output image of fixed size, image storage space in memory for all non-median rendering types is O(1) in the number of input frames and O(n) in the number of pixels per input frame, since at most one input image is loaded into memory at any time. For median-value rendering, storage is O(n) in the number of input frames. When using projectively-aligned input images, however, renderings that accommodate all regions of all input images can generate arbitrarily large output for a bounded input size, and can use an arbitrarily large amount of memory.

Alignment Algorithm

Details on the alignment algorithm used in ALE are here.

3D Scene Reconstruction

The scene reconstruction code is still very experimental and is not currently covered by this document. For more information, see the user manual and source code.